Se tester

QCM 1
QCM 2
Exercices

QCM 1

QCM

1) Que signifient les initiales GCM ?
General Circulation Model
Global Climate Model
Global Circulation Model
Global Circulation Monitor

QCM

1) Pourquoi utilise-t-on un GCM pour simuler l'atmosphère des exoplanètes ?
Pour savoir avec précision le temps qu'il fera demain en un point précis de la planète.
Pour faire des études du climat selon divers paramètres.
Les deux réponses précédentes.
Personne ne sait vraiment pourquoi.

2) Usuellement, comment appelle-t-on les deux constituants majeurs d'un GCM ?
Physique et Dynamique
Mécanique et Dynamique
Mécanique et Atmosphérique

QCM 2

Exercices

Exercice

Question 1)

Vous oubliez de brancher la physique dans votre GCM de planète tellurique. Que peut-il se passer au niveau des résultats ?

Exercice

Question 1)

Vous avez un modèle de dimension N_longitude x N_latitude et vous passez 2N_longitude x 2N_latitude. Que faut-t-il faire pour respecter la condition CFL ? A priori, par combien sera multiplié le temps de calcul ?

Question 2)

On souhaite simuler avec un GCM une atmosphère de diazote pour une planète d'un rayon de 6000 km. On sait par ailleurs, en considérant le flux radiatif de l'étoile et sa distance à la planète, que la température maximale dans cette atmosphère n'excèdera pas 400 K. On demande à un étudiant d'effectuer une première simulation de cette atmosphère. L'étudiant propose d'utiliser une grille latitude-longitude avec 100 points en longitude et 100 points en latitude et un pas de temps dynamique de 20 minutes. On lui répond que sa simulation échouer. Pourquoi cela ?

Réponses aux QCM

pages_gcm-se-tester/gcm-qcm1.html

QCM

Question 1
Solution : réponse 1) ( Bien que correct, on préfère employer le terme de Climat à celui de Circulation car il reflète mieux l'usage d'un GCM pour une exoplanète. De plus, l'usage préfère le mot Global à Général. )
Solution : réponse 2)
Solution : réponse 3) ( Bien que correct, on préfère employer le terme de Climat à celui de Circulation car il reflète mieux l'usage d'un GCM pour une exoplanète. )

pages_gcm-se-tester/gcm-qcm1.html

QCM

Question 1
Solution : réponse 2)
Question 2
Solution : réponse 1)

pages_gcm-se-tester/gcm-questions-qcm2.html

QCM 'Question de cours'

Question 1
Solution : réponse 3)
Question 2
Solution : réponse 3) ( C'est vraiment la limite basse, qui est plutôt employée pour la Terre, dans des applications de prédiction météorologique. )
Solution : réponse 4)
Question 3
Solution : réponse 4)
Question 4
Solution : réponse 1)

Réponses aux exercices

pages_circulation-globale/gcm-exercices.html

Exercice

Question 1
Solution :
Sans physique, on ne tient pas compte du transfert radiatif, donc on ne tient pas compte de l'ensoleillement qui varie avec la latitude. Dans ce cas, la circulation à grande échelle entre l'équateur et les pôles ne se fera pas si on part d'un état atmosphérique au repos.

pages_circulation-globale/gcm-exercices.html

Exercice

Question 1
Solution :
Il faut diminuer le pas de temps par un facteur 2. A noter qu'il n'y a pas besoin de changer le nombre de niveaux verticaux. Le temps d'éxécution total sera alors multiplié par 2x2x2 = 8.
Question 2
Aide :
Calculer la vitesse de l'onde la plus rapide ...

Aide :
... puis appliquer la condition CFL.

Solution :
La question ici est de savoir si la simulation numérique sera stable, en s'assurant que la condition CFL sera respectée. Pour cela on calcule la vitesse du son, qu'on comparera aux pas de temps spatial et temporel.

En considérant un gaz parfait, on a un coeffcient adiabatique 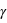égal à 1.4. La vitesse du son étant égale à , avec 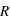la constante des gaz parfaits et 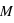la masse molaire du diazote (28 g/mol), on obtient que la vitesse du son est au maximum de 408 m/s.

La distance entre deux points de maille est maximale à l'équateur et vaut 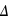x = 377 km. Le nombre de Courant pour un pas de temps de 20 min donne C = 1.3, la simulation n'est donc pas stable. En un pas de temps, une onde sonore se déplacera de plus que une maille physique.